降圧コンバータ(降圧チョッパ)の出力電圧の制御方法として、電圧モード制御(VMC)がある。今回、Type3補償器を用いた降圧コンバータのフィードバック制御をLTspiceでシミュレーションしてみる。
降圧コンバータのパラメータ設定と伝達関数
降圧コンバータのパラメータ設定は以下とする。
$$ \begin{align}
&V_{in}=100 \,\text{V} \\
&V_{o}=70 \,\text{V} \\
&L=200 \,\mu\text{H} \\
&C=100 \,\mu\text{F} \\
&f_s=100 \,\text{kHz} \\
\end{align} $$
また、降圧コンバータの伝達関数\(G_{DVo}\)(ディーティ比:Dに対する出力電圧Voの伝達関数)は、よく知られていて以下となる。
$$ \begin{align}
G_{DVo}(s) &= \frac{\Delta V_o(s)}{\Delta D(s)} = \frac{V_{in}}{L C s^2 + \frac{L}{R} s + 1} \
\end{align} $$
降圧コンバータの電圧モード制御(VMC)シミュレーションモデル
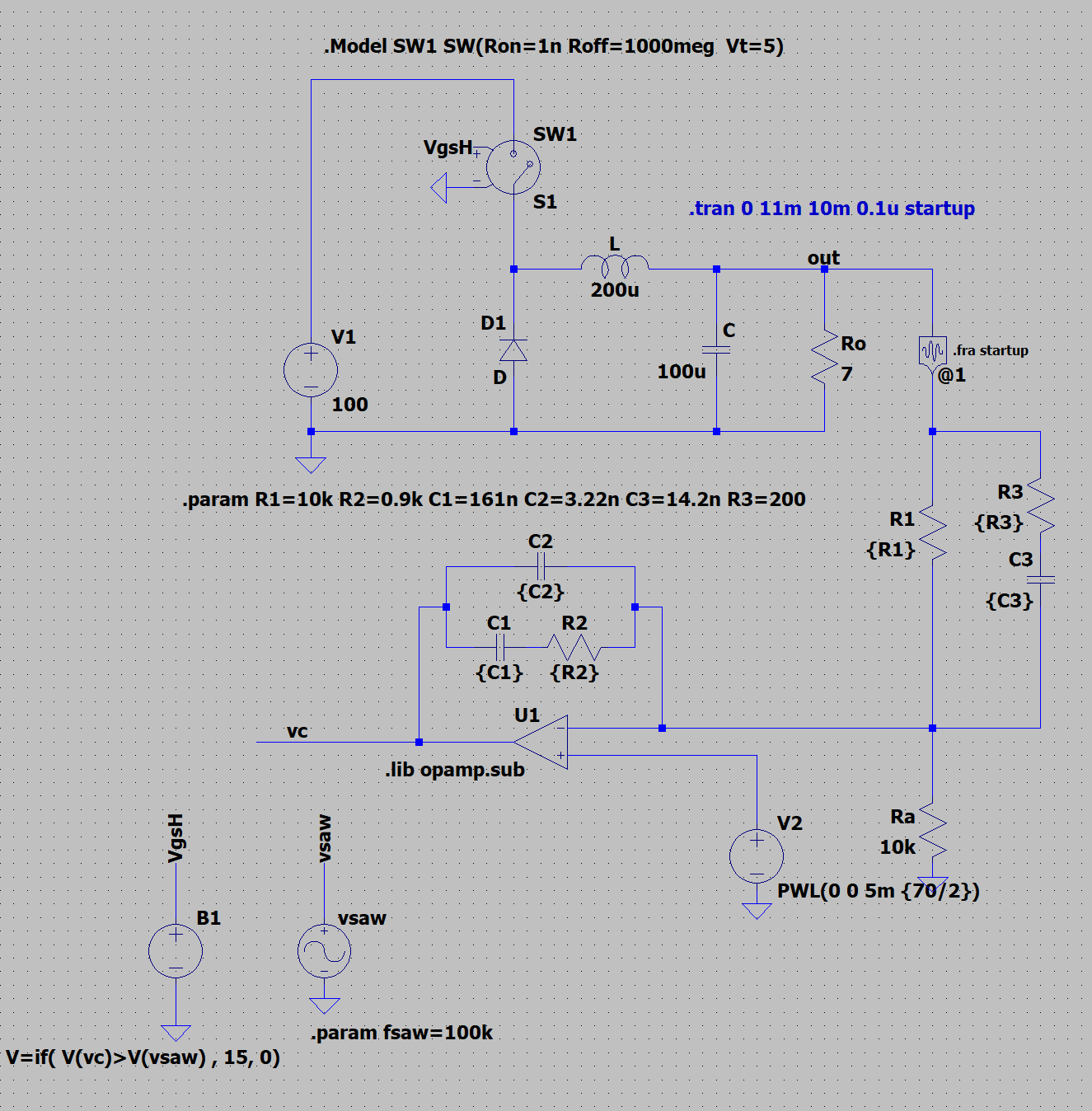
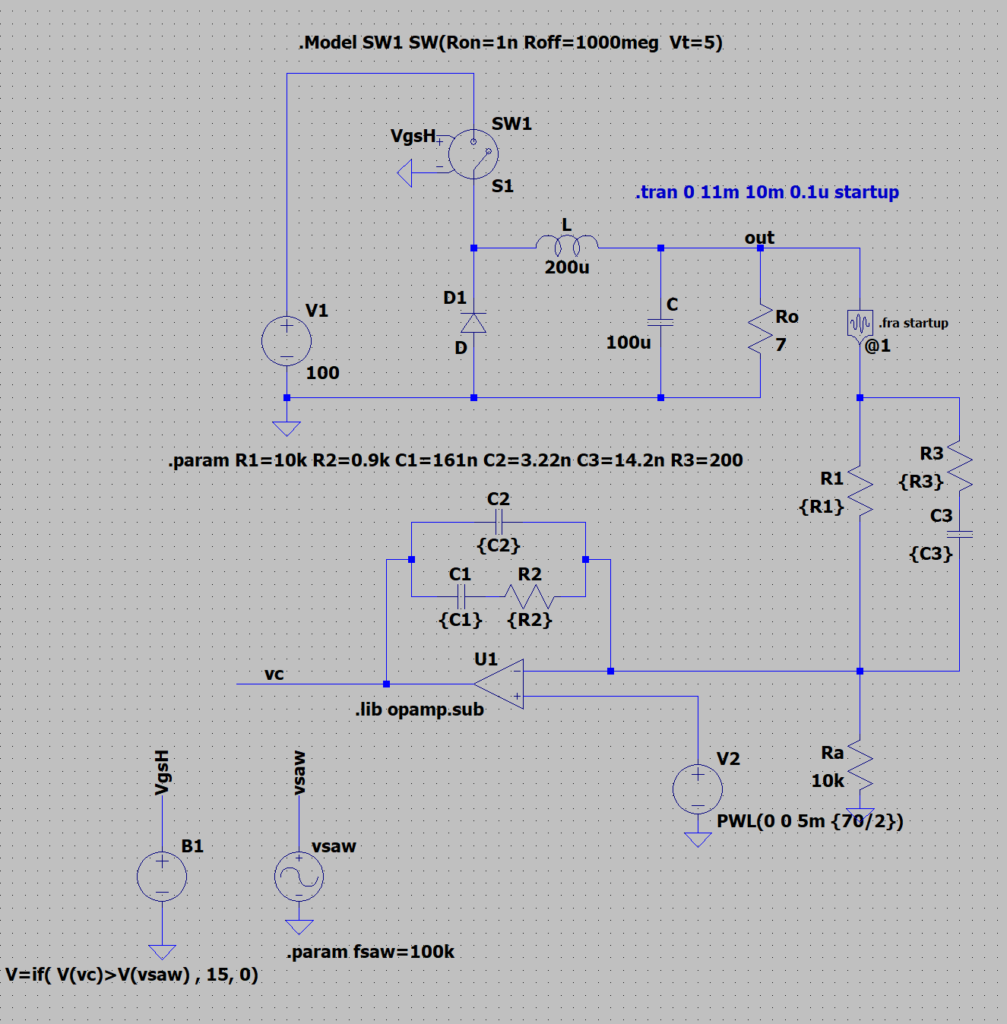
降圧コンバータの電圧モード制御(VMC)シミュレーションモデルを以下に示す。
降圧コンバータ制御の一巡伝達関数
制御設計する場合、制御ループを一周した時の一巡伝達関数\(G_{loop}\)を考える必要がある。降圧コンバータ制御のブロック線図を以下に示す。
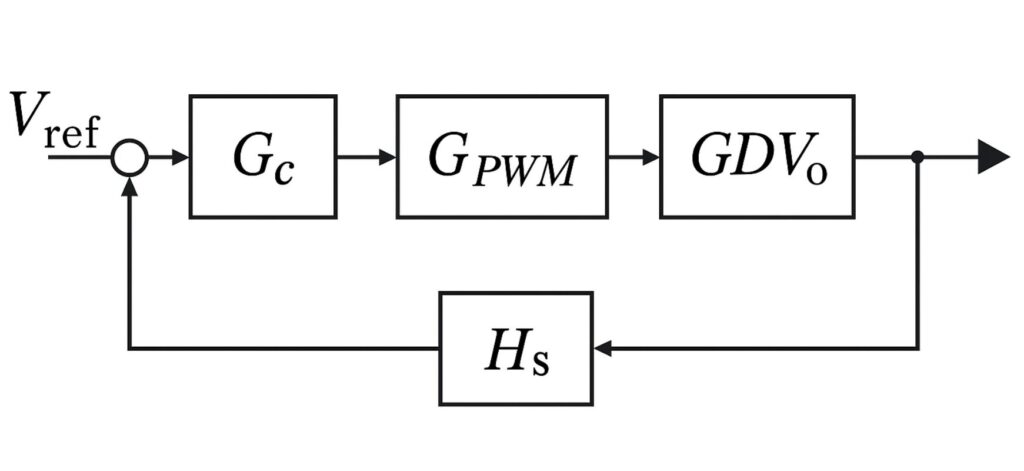
一巡伝達関数\(G_{loop}\)は以下のようになる。
$$ \begin{align}
&G_{loop}=G_{DVo}G_{c}G_{pwm}H_s
\end{align} $$
なお、\(G_{c}\)は位相補償器の伝達関数(今回はType3)、\(G_{pwm}\)はPWMゲインである。Hsはセンサゲインであるが、今回のように抵抗分圧部(R1とRa)がオペアンプの位相補償器(Type3)に含まれる場合は、センサゲインHsは不要となる(Raに無関係になる)。
\(G_{pwm}\)はPWMゲインは以下となる。
$$ \begin{align}
&PWMゲイン:G_{pwm}=\frac{1}{Vpp} \,(Vppはのこぎり波の振幅値) \\
\end{align} $$
Type3補償器の設計(Scilabで実施)
Type3補償器を設計する。今回は、Scilabを用いてボード線図を描いてもらい、仕様の制御系になるよう定数を調整した。
制御系の仕様は以下とする。制御系は様々な書籍で書かれている指標(経験則)に従って設定した。クロスオーバー周波数fgcは、スイッチング周波数fsの1/10とした。
$$ \begin{align}
&クロスオーバー周波数f_{gc}=10 \,\text{kHz} \\
&位相余裕=50 \text{°}以上 \\
&ゲイン余裕=6 \text{dB}以上 \\
\end{align} $$
設計手順(大雑把なやり方)
ロジカルに設計する方法もあるが、今回は大雑把なやり方で設計していく。
①
今回は簡単のため、R1とRaによる分圧比を1/2とした(通常は検出ICの定格電圧以下にする)。よって、R1は以下となる。
$$ \begin{align}
&R_1=10 \,k\Omega
\end{align} $$
②
零点周波数fz1, fz2は、降圧コンバータLCの共振周波数に設定する(いい感じになる)。極周波数fp1, fp2は、一先ず零点周波数の50倍に設定する(必要があれば後で調整する)。Type3ゲインGoも一先ずGo=1に設定する(後で調整することが多い)。
$$ \begin{align}
&f_{z1}, f_{z2}=\frac{1}{2\pi\sqrt{LC}}=1.1 \,kHz\\
&f_{p1}, f_{p2}=1.1 \times 50=56 \,kHz\\
&G_o=1
\end{align} $$
③
Scilabで出力した一巡伝達関数の周波数特性を示す。目標仕様のクロスオーバー周波数:10 kHzで位相余裕:59度、ゲインは+21.09 dBとなっている。
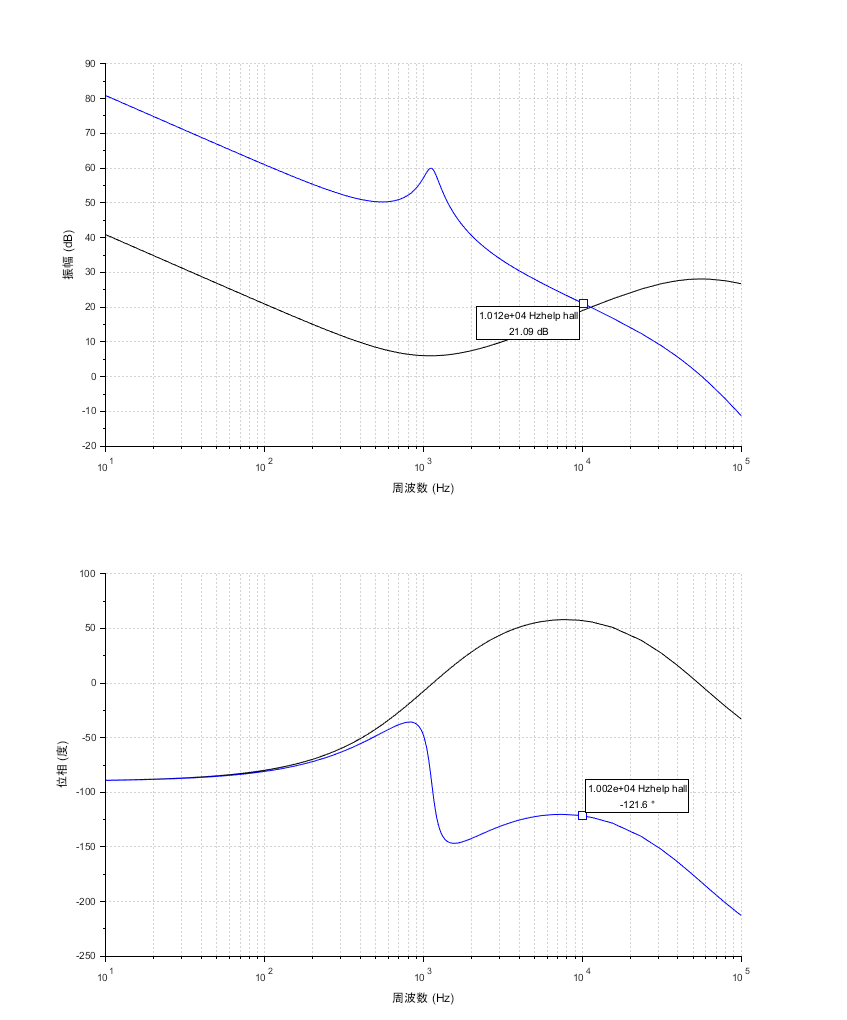
ここからゲインを調整して、クロスオーバー周波数を10 kHzに持ってくる。ゲインが+21.09 dBなので、Type3ゲインGoを調整して、全体のゲインが-21.09dBになるようにする。Type3ゲインGoは、以下の式で求められる。
$$ \begin{align}
&G_o=1(元のゲイン) \times 10^\frac{-21.09}{20}=0.09
\end{align} $$
したがって、抵抗R2は以下の式で求められる(Type3ゲインGo=R2/R1に近似)。
$$ \begin{align}
&R2=0.09 \times 10k\Omega(R1)=0.9 \, k\Omega
\end{align} $$
ゲインGoを修正して、Scilabで出力した一巡伝達関数の周波数特性を示す。目標仕様のクロスオーバー周波数:10 kHzで位相余裕:59度、ゲインは0 dBとなっている。
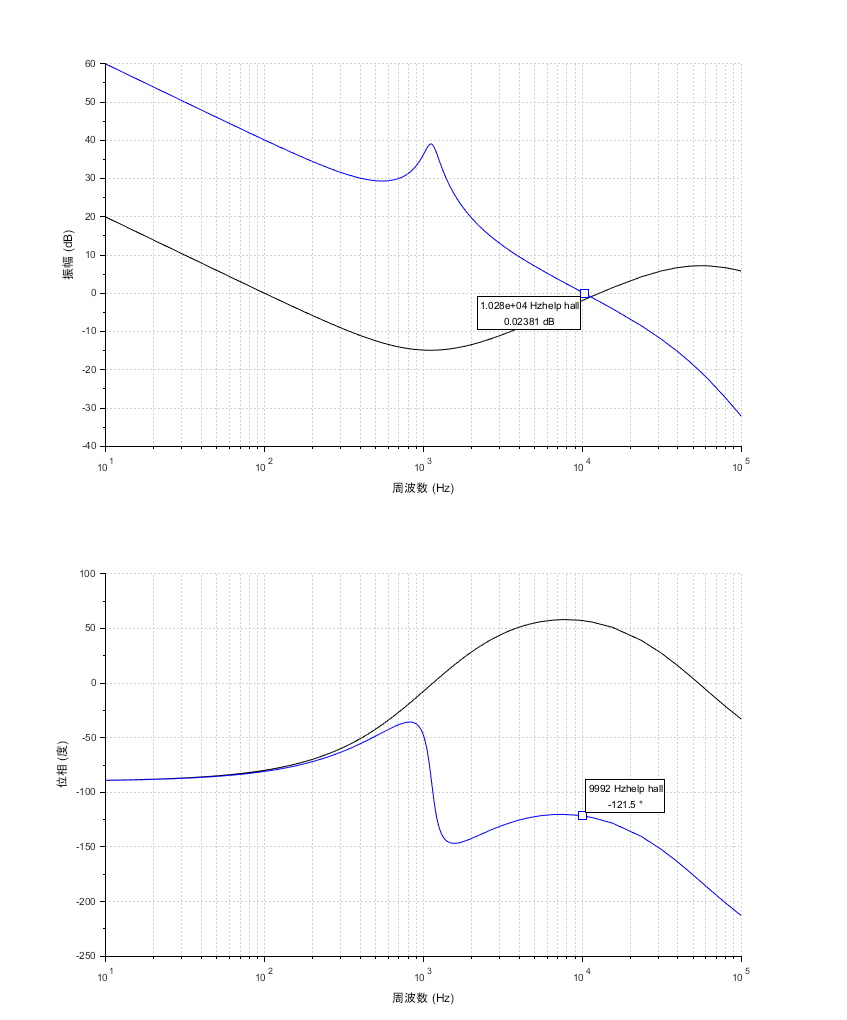
④
上記で求めたR1、R2の値と設定した零点周波数fz1、fz2と極周波数fp1、fp2より、オペアンプを用いたType3補償器の定数を決定する(数式は別記事参照)。
オペアンプを用いたType3補償器の定数を以下に示す。
$$ \begin{align}
R_1 &= 10 \,k\Omega \\
R_2 &= 0.9 \,k\Omega \\
C_1 &= 161 \,nF \\
C_2 &= 3.22 \,nF \\
C_3 &= 14.2 \,nF \\
R_3 &= 200 \,\Omega
\end{align} $$
LTspiceでのFRAシミュレーション結果
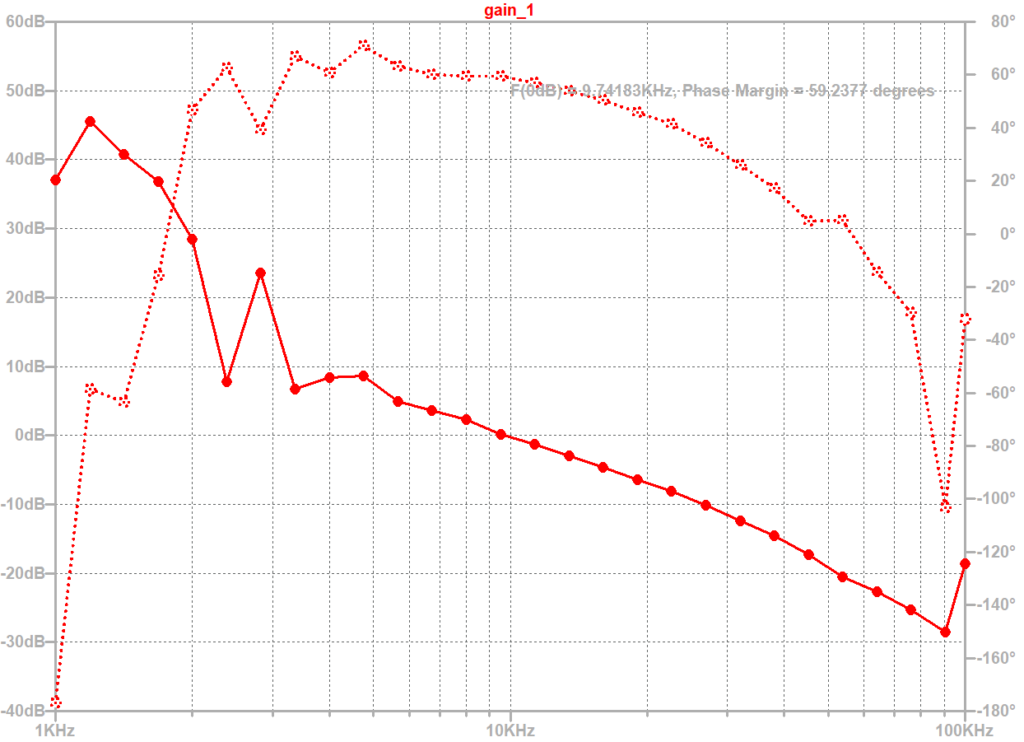
LTspiceでのFRAシミュレーション結果を示す。
クロスオ-バー周波数は9.7kHz、位相余裕は59度、ゲイン余裕は20dB程度となった。先ほどの設計値と比較して、概ね一致する結果となった(低周波でゲインがガタつくのは別途検討したいと思います)。
参考:Scilabコード
//降圧コンバータ制御設計
s=poly(0,'s');
clf();
//****** 降圧コンバータのパラメ-タ- ******
Vi = 100; // 入力電圧
Vo = 70; // 出力電圧
R = 7; // 負荷抵抗値
L = 200*10^-6; // インダクタンス
C = 100*10^-6; // 出力容量
D = Vo / Vi; // デューティ比
fs = 100*10^3 // スイッチング周波数
Vpp = 1; // PWMの振幅
//****** 降圧コンバータ伝達関数 ******
Gdvo = syslin('c',Vi/(1+L*s/R+L*C*s^2)) // デューティ比から出力電圧への伝達関数
//****** Type3 補償器の伝達関数 ******
Go = 0.09; // Type3 制御器のゲイン
fz1 =1.1*10^3; // Type3 零点周波数
fz2 =1.1*10^3; // Type3 零点周波数
fp1 =56*10^3; // Type3 極周波数
fp2 =56*10^3; // Type3 極周波数
Gc3 = syslin('c',Go*(1+2*%pi*fz1/s)*(1+s/(2*%pi*fz2))*(1+s/(2*%pi*fp1))^-1*(1+s/(2*%pi*fp2))^-1); // Type3 補償器の伝達関数
//****** 一巡伝達関数 ******
bode([Gc3;Gc3*1/Vpp*Gdvo],10,100*10^3)
//Type3補償器設計
clear;
s=poly(0,'s');
clf();
fz1 =1.1*10^3; // 零点周波数
fz2 =1.1*10^3; // 零点周波数
fp1 =56*10^3; // 極周波数
fp2 =56*10^3; // 極周波数
//抵抗値
R1 = 10*10^3;
R2 = 0.9*10^3;
// ω = 2πf
omega1z = 2 * %pi * fz1;
omega2z = 2 * %pi * fz2;
omega1p = 2 * %pi * fp1;
omega2p = 2 * %pi * fp1;
// 各コンデンサ値の計算
C1 = 1 / ( 2 * %pi * fz1 * R2);
C2 = C1 / (2 * %pi * fp1 * C1*R2-1);
C3 = (fp2 - fz2) / (2 * %pi * R1* fp2 * fz2);
R3 = R1 * fz2/(fp2 - fz2);
// オペアンプでのType3補償器
Gc1 = syslin('c', R2/R1* C1/(C1+C2) * (1+1/(s*R2*C1))*(1+s*(R1+R3)*C3)*(1+s*R2*C1*C2/(C1+C2))^-1*(1+s*R3*C3)^-1)
// Type3補償器(参考比較)
K = R2/R1* C1/(C1+C2);
Gc3 = syslin('c',K*(1+2*%pi*fz1/s)*(1+s/(2*%pi*fz2))*(1+s/(2*%pi*fp1))^-1*(1+s/(2*%pi*fp2))^-1);
bode([Gc1; Gc3],100,10*10^6);
// 表示
format('e', 10);
disp("計算されたコンデンサ値 [F]:");
disp("C1 = " + string(C1));
disp("C2 = " + string(C2));
disp("C3 = " + string(C3));
disp("R3 = " + string(R3));
disp("fz1 = " + string(1/( 2 * %pi* R2*C1)));
disp("fz2 = " + string(1/( 2 * %pi* (R1+R3)*C3)));
disp("fp1 = " + string(1/( 2 * %pi* R2*C1*C2/(C1+C2))));
disp("fp2 = " + string(1/( 2 * %pi*R3*C3)));