PID制御は、電気機器においてメジャーに使用される制御方法です。PID制御器は、オペアンプを用いて実現できる。
今回、オペアンプを用いたPID制御器について各部品の定数決定方法と、PID制御器のデジタル化について記載します。
PID制御器の回路図と伝達関数
オペアンプを用いたPID制御器の回路図は以下のようになる。
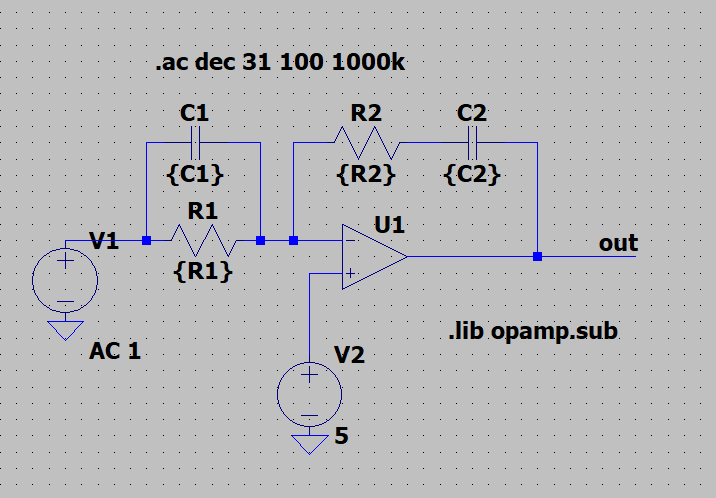
また、PID制御器の伝達関数G_cは以下で表される。
$$ \begin{align}
G_c &= K_p + \frac{K_i}{s} + K_D s \\
& = K_p \left( 1 + \frac{1}{T_i s} + T_d s \right)
\end{align} $$
なお、\( T_i=K_p/K_i\)、\( T_d=K_d/K_p\)とした。
各定数は以下の式で表される。
$$ \begin{align}
\textbf{比例ゲイン} \quad
& K_p = \frac{R_2}{R_1} \\
\textbf{積分時間} \quad
& T_i = R_2 C_2 \\
\textbf{1つ目の折点周波数} \quad
& f_1 = \frac{1}{2\pi T_i} = \frac{1}{2\pi R_2 C_2} \\
\textbf{積分ゲイン} \quad
& K_i = \frac{K_p}{T_i} = \frac{R_2}{R_1} \cdot \frac{1}{R_2 C_2} = \frac{1}{R_1 C_2}\\
\textbf{微分時間} \quad
& T_d = R_1 C_1 \\
\textbf{2つ目の折点周波数} \quad
& f_2 = \frac{1}{2\pi T_d} = \frac{1}{2\pi R_1 C_1} \\
\textbf{微分ゲイン} \quad
& K_d = K_p T_d = \frac{R_2}{R_1} \cdot R_1 C_1 = R_2 C_1
\end{align} $$
PID制御器の周波数特性を折れ線近似で描くと、以下のようになる。
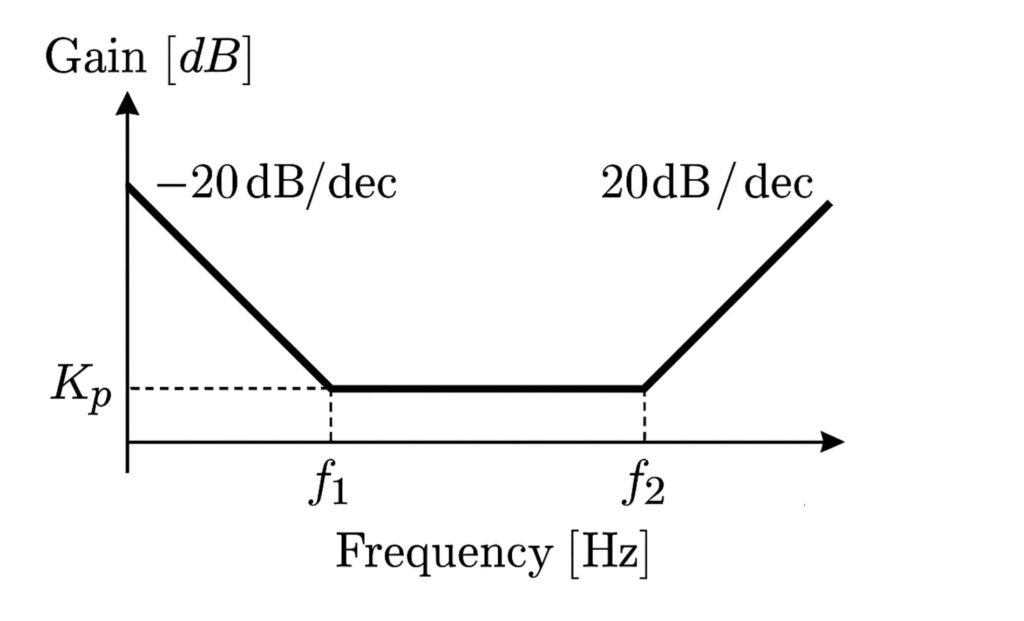
各定数を設計して、LTspiceで周波数特性を確認
比例ゲイン:Kp=1、R1=1 kΩ、折点周波数:f1=1 kHz、折点周波数:f2=100 kHzとすると、その他の定数は上式を用いて以下のように決定できる。
$$ \begin{align}
&R1=1 \,k\Omega \\
&R2= \frac{R_1}{K_p} =1 \,k\Omega \\
&C1= \frac{1}{2\pi R_1 f_2}=1.59 \,nF \\
&C2= \frac{1}{2\pi R_2 f_1}=159 \,nF \\
\end{align} $$
決定した定数を入れて、LTspiceのAC解析で周波数特性を取得した。シミュレーション結果を見ると、設計したPID制御器の特性が実現できていることが確認できた。
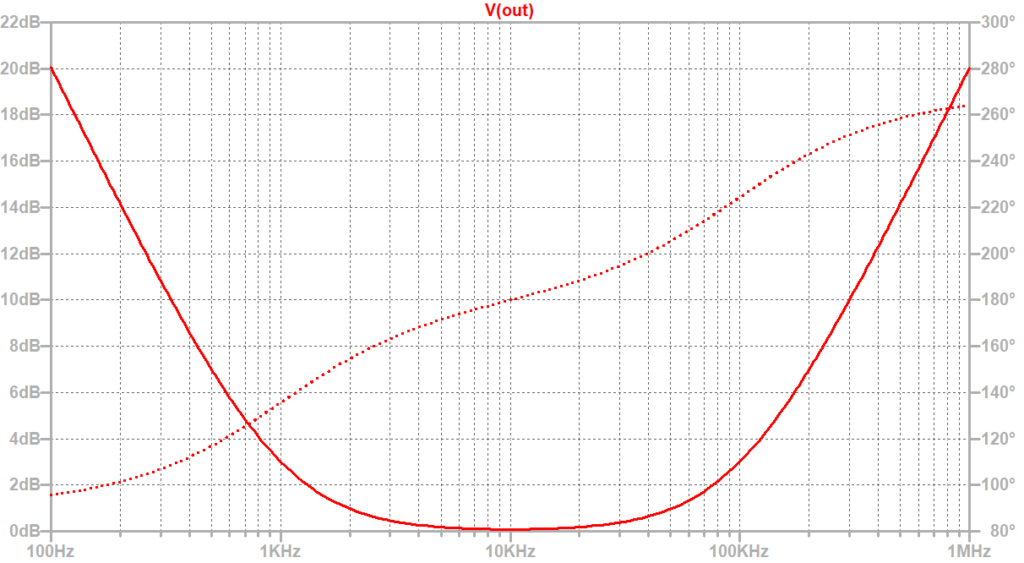
PID制御器をデジタル化してみる。
デジタル化するためには、s領域の伝達関数をz領域に変換(離散化)する必要がある。s領域からz領域に変換する方法は、主に前進オイラー法、後進オイラー法、双一次変換がある。
今回は変換精度の高い双一次変換を用いる。双一次変換は次式で表せる。
$$ \begin{align}
s = \frac{2}{T_s} \cdot \frac{1 – z^{-1}}{1 + z^{-1}}
\end{align} $$
なお、\( T_s\)はADコンバータ等のサンプリング周期である。
この双一次変換の式をPID制御器の伝達関数に代入し、s関数を消去してz関数に変換すると次式になる(途中式は割愛します。)。
$$ \begin{align}
&Y[n] =Y[n-2]+A1 \cdot E[n] +A2 \cdot E[n-1] +A3 \cdot E[n-2]\\
ただし、\\
&A1=K_p + \frac{K_i T}{2} + \frac{2K_d}{T} \\
&A2=K_i T – \frac{4K_d}{T} \\
&A3=-K_p + \frac{K_i T}{2} + \frac{2K_d}{T}\\
とする。
\end{align}$$
なお、括弧内の[n-1]や[n-2]は、1個前のサンプル値、2個前のサンプル値を表す。
デジタルPID制御器をLTspiceでシミュレーション
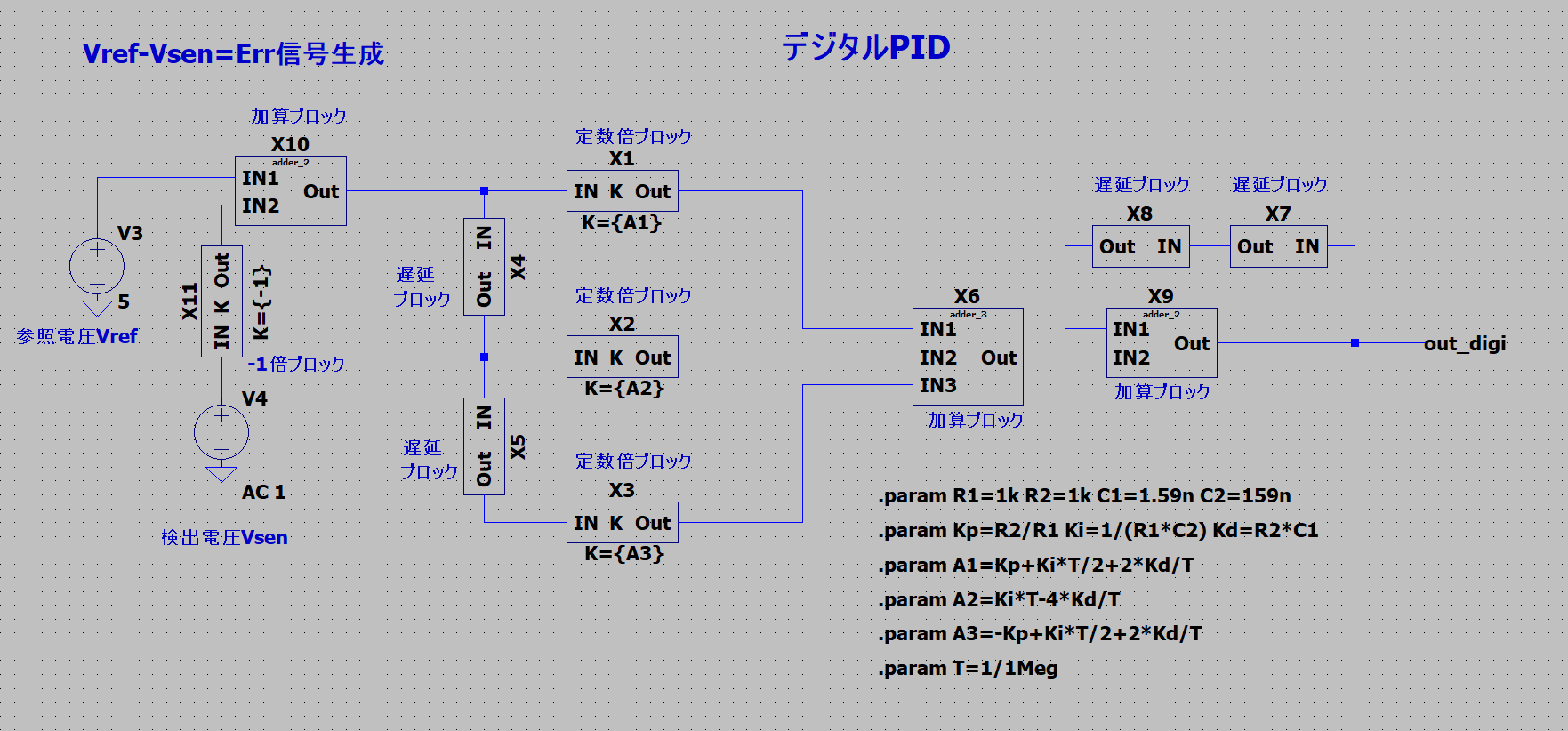
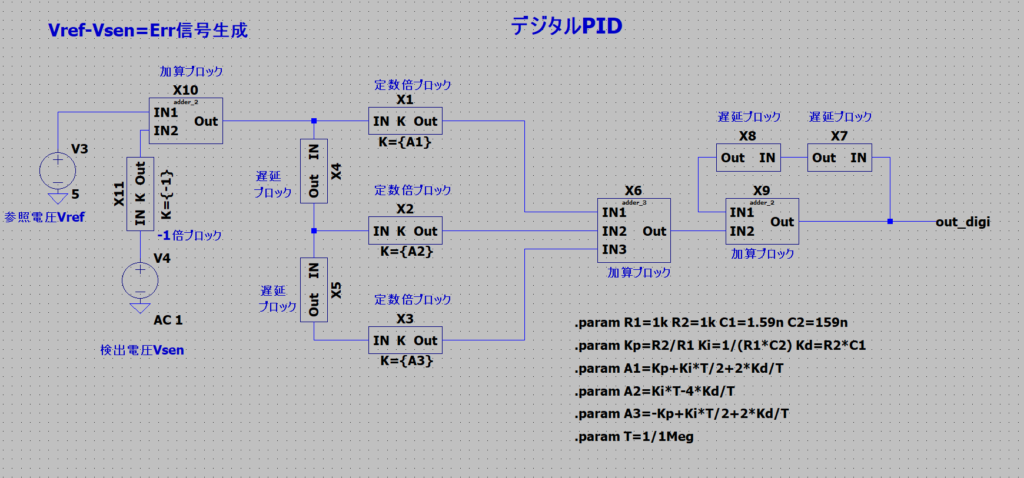
上記の式をブロック図にすると、下記のLTspice回路のようになる。各ブロックについては、自作で作成した。
設計条件は先ほどと同様に、比例ゲイン:Kp=1、折点周波数:f1=1 kHz、折点周波数:f2=100 kHzとし、サンプリング時間:Ts=1us(1 MHz)とした。
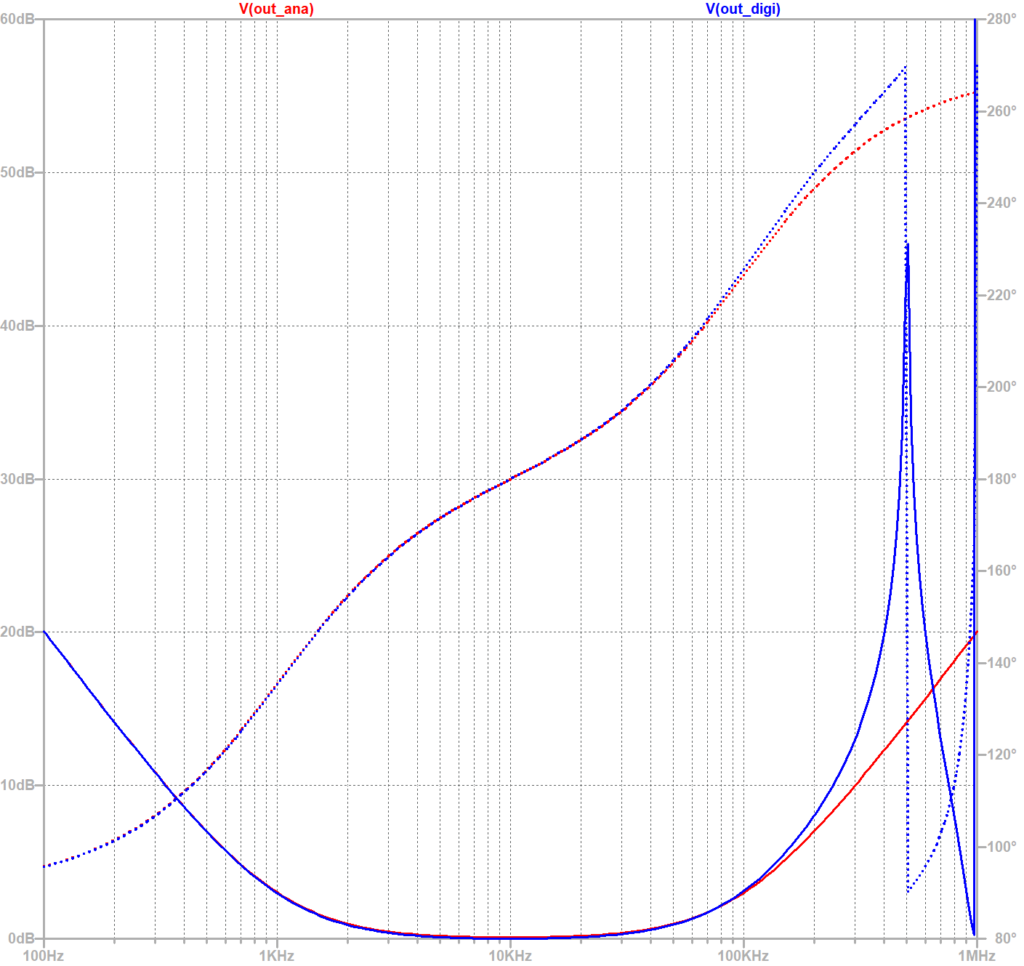
オペアンプを用いたアナログPID制御器(赤線)とデジタルPID制御器(青線)の周波数特性をシミュレーションで比較した。図のようにほぼ一致した特性となることが確認できた。
デジタルPID制御器(青線)では、500 kHz以降で波形が乱れている。これは、サンプリング周波数が1 MHzのため、その1/2周波数である500 kHz(ナイキスト周波数)以降では波形が正しく生成できないためである(ナイキストの定理)。